[오늘의 일지]
기초 수학 및 기초 통계학 - 이항정리, 지수함수, 확률분포, 샘플링, 수열과 극한, CLT and LLN
[상세 내용]
기초 수학 및 기초 통계학
이항정리
- Factorial : 보통 n∈N, n! 은 아래와 같이 정의한다. 파이 모양의 문자가 곱연산을 의미한다고 나와있다. 특이한 점은 '0! := 1'이라고 정의하는데 증명과정은 다음과 같다. ' n! = n(n-1)! → n!/n = (n-1)! → n = 1 대입 → n!/1 = 0! → 1 = 0! '

- Binomial theorem : 이항정리라고 말하며 식은 다음과 같다. 그냥 보면 이해가 잘 되지는 않지만 이항 계수를 보고 오면 이해가 쉽다.

- Binomial coefficient : (a+b)^n의 다항식을 전개했을 때 모든 식을 풀지 않고 각각의 계수를 구할 수 있는데 그것이 이항계수이다. 아래와 같이 증명된다. 또한 고등학교 때 배우는 nCr(n Combination r) 같은 의미를 하고 있다.

- 파스칼의 삼각형 : 이항정리에서 이항계수를 삼각형으로 나타낸 그림이다. 하나씩 더하면서 내려가는 규칙이 있다.

- Multinomial theorem : 위에서는 단 2개의 항만 가지는 이항에 관련된 정리였다면 당연하게도 다수의 항을 가지는 다항식의 정리도 존재한다. 또한 다항계수도 구하는 식이 존재한다. 여기까지 수업을 들으면서 각각의 특정 항의 계수를 구하는 것이 확률적인 특징을 가지고 팩토리얼을 통해서 구해진다는 것을 다시 한번 이해할 수 있었다.

지수함수
- 지수함수 파트에서는 sin함수를 예시로 지수함수의 축소, 확대, 평행이동에 대해서 수업을 해주셨는데 보통 y = f(x)의 형태를 기본으로 할 때 y - b = f(x-a)나 y = f(ax), y = af(x)를 예시로 보여주셨다. 평행이동은 그냥 a, b 만큼 이동하는 것으로 이해가 간단한데 f(ax)나 af(x)는 그래프를 보면서 이해하면 f(ax)는 1/a만큼 축소하고 af(x)는 y축 방향으로 a배 증가한다는 것을 알 수 있었다.

- 지수함수와 로그함수의 극한

- Euler's Number : 조합론에서 오일러 수 또는 자연상수 e는 주어진 개수의 역행을 가지는 순을 세는 수이다. 정의는 다음과 같다.
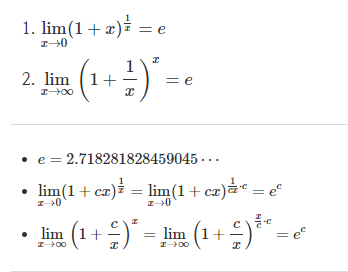
확률분포
- 이항분포(binomial distribution)

- 다항분포(multinomial distribution)

- 정규분포(normal distribution) : 통계학에서 정규분포(normal distribution) 또는 가우스 분포(Gaussian distribution)는 PDF(연속 확률분포)의 하나이다. 정규분포는 수집된 자료의 분포를 근사하는 데에 자주 사용되며, 이것은 중심극한정리에 의하여 독립적인 확률변수들의 평균은 정규분포에 가까워지는 성질이 있기 때문이다. 정규분포는 2개의 매개 변수 평균 μ과 표준편차 σ에 대해 모양이 결정되고, 이때의 분포를 N(μ,σ^2)로 표기한다. 특히, 평균이 0이고 표준편차가 1인 정규분포 N(0,1)을 표준 정규 분포(standard normal distribution)라고 한다.

- 푸아송분포(Poisson distribution)

샘플링
- 간략하게 정리하자면 모집단으로부터의 샘플링을 하는 표본은 모집단의 분포를 추정하는 것을 목표로 한다.
수열과 극한
- 해석학에서, 수열의 극한은 수열이 한없이 가까워지는 값이다. 직관적으로, an이 n이 커짐에 따라 어떤 고정된 값 a에 제한이 없이 가까워진다면, (an)이 a로 수렴한다고 하며, a를 (an)의 극한이라고 한다. 어디로도 수렴하지 않는 수열을 발산한다고 한다. 예를 들어, 수열 (1/n)은 0에 한없이 가까워지므로 수렴하며, 그 극한은 0이다. 반면 수열 ((-1)^n)은 어떤 고정된 값에 한없이 가까워지지 않으므로 발산한다. 수열의 극한의 개념은 실수 공간을 비롯한 거리 공간을 비롯한 위상 공간에서 논의할 수 있다.
CLT and LLN
- CLT : 무작위로 추출된 표본의 크기가 커질수록 표본 평균의 분포는 모집단의 분포 모양과는 관계없이 정규분포에 가까워진다는 정리. 이때 표본 평균의 평균은 모집단의 모 평균과 같고, 표본 평균의 표준 편차는 모집단의 모 표준 편차를 표본 크기의 제곱근으로 나눈 것과 같다. 큰 수의 법칙과는 상보적인 관계에 가까운데, 확률수렴이 분포수렴보다 더 강력한 개념이기 때문에 큰 수의 법칙이 더 강력한 결과라고 오해할 수도 있으나, 중심극한정리는 점근적인 분포가 정규확률분포라는 추가적인 정보까지 제시해 주기 때문에 두 법칙 간에 상하관계가 존재한다고 할 수는 없다. 큰 수의 법칙은 표본평균이 모평균으로 확률수렴한다는 이야기이며, 중심극한정리는 표본평균의 분포가 "어떤 모양"을 가지고 수렴하는지에 관해 이야기하는 것이 그 핵심이다. 표본평균이 모평균에 얼마나 빠르게 수렴하는지, 그 수렴 속도에 관해 이야기하는 법칙은 반복된 로그의 법칙(law of iterated logarithm)이라고 불린다.
- LLN : 큰 수의 법칙(law of large numbers, LLN)은 경험적 확률과 수학적 확률 사이의 관계를 나타내는 법칙으로, 표본집단의 크기가 커지면 그 표본평균이 모평균에 가까워짐을 의미한다. 따라서 취합하는 표본의 수가 많을수록 통계적 정확도는 올라가게 된다.
용어정리
A ⇢ B ⇔ f : A' → B for some A' ⊂ A
convergence : 수렴
saturation : 포화
i.i.d : independent and identically distributed로서 확률변수가 여러 개 있을 때 (X1 , X2 ,... , Xn) 이들이 상호독립적이며, 모두 동일한 확률분포 f(x)를 가진다면 iid이다.
기댓값 E(x) : 기댓값 (Expected Value)은 어떤 확률 과정을 무한히 반복했을 때 얻을 수 있는 값들의 평균으로 기대하는 값으로 중심적 성향 또는 분포의 무게중심을 알려
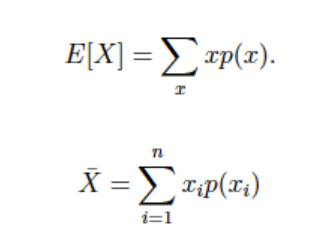
분산 Var(x) : 분산이란 변수의 흩어진 정도를 계산하는 지표로 통계에서 주어진 변량이 평균으로부터 떨어져 있는 정도를 나타내는 값의 한 종류입니다.
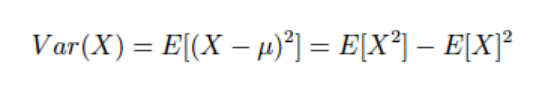
[마무리]
오늘 수업은 전체적으로 어려운 내용을 빠르게 많은 양을 넣으려고 해서 그런지 어느 순간부터는 집중력이 많이 떨어졌고 그냥 '이런 내용이 있다'라는 식의 느낌으로 흘러갔던 거 같습니다. 차후에 복습이 필요할 것 같습니다.
'AI > 기초 이론' 카테고리의 다른 글
| [AI 부트캠프] DAY 6 - 기초 통계학 및 수학 이론 강의 5 (0) | 2023.07.24 |
|---|---|
| [AI 부트캠프] DAY 5 - 기초 통계학 및 수학 이론 강의 4 (0) | 2023.07.22 |
| [AI 부트캠프] DAY 3 - 기초 통계학 및 수학 이론 강의 2 (0) | 2023.07.20 |
| [AI 부트캠프] DAY 2 - 기초 통계학 및 수학 이론 강의 1 (1) | 2023.07.19 |




댓글