[오늘의 일지]
통계학 기초 정리 - 통계 실험과 유의성 검정, 선형회귀분석
기초 수학 및 통계 - 함수, 확률 기초
[상세 내용]
통계학 기초정리
통계 실험과 유의성 검정
- 가설검정 : 검정이라는 말은 영어로 test로 내가 세운 가설을 통계적으로 유의한 지 살펴보는 것을 의미한다. 검정의 순서는 귀무가설과 대립가설을 설정한 뒤 p-value를 구하고 p-value를 기준으로 가설의 채택/기각 여부를 결정한다.
- 귀무가설(Null hypothesis:H0) : 검정의 대상이 되는 가설로서 보통 기존의 관습적이고 보수적인 가설이다. 귀무가설은 기각(reject)을 목표로 한다.
- 대립가설(Alternative hypothesis: H1) : 귀무가설에 대립되는 가설로서 연구자가 원하는 주장에 해당한다. 대립가설은 채택(accept)을 목표로 한다.
- p-value : 의미는 유의확률로서 귀무가설이 맞다고 가정할 때 얻은 결과보다 극단적인 결과가 실제로 관측될 확률이다. 보통 비교로 사용될 때 기준은 0.05 보다 크거나 작은 것으로 기각과 채택을 결정한다.
- 단측 검정(one-tailed test) : 한 방향성으로 가능성이 크다고 생각될 때 사용된다.
- 양측 검정(two-tailed test) : 방향성은 모르겠지만 차이가 있다고 생각될 때 사용된다. 즉 비교 대상이 특정하지 않지 않을 때 사용된다.

- 제1종 오류 : '귀무가설'이 옳은데도 불구하고 이를 기각하는 오류로서 우연에 의한 효과를 실제 효과라고 잘못 결론 내린 것이라고 볼 수 있다.
- 제2종 오류 : '귀무가설'이 옳지 않은데도 이를 채택한 오류로서 실제 효과를 우연에 의한 효과라고 잘못 결론 내려서 발생한 것이다. 1종과 2종 오류를 비교해 보면 2종 오류가 더 치명적이라고 할 수 있다.
- t 검정(t test) : 모집단의 분산이나 표준편차를 알지 못할 때 모집단을 대표하는 표본으로부터 추정된 분산이나 표준편차를 가지고 검정하는 방법으로 "두 모집단의 평균 간의 차이는 없다"라는 귀무가설과 '두 모집단의 편균 간에 차이가 있다'라는 대립가설 중에 하나를 선택할 수 있도록 하는 통계적 검정방법이다. t 검정도 t-value을 기준으로 기각영역이 존재한다. 여기서 t-value이란 검정통계량으로, 두 집단의 차이의 평균을 표준오차로 나눈 값이다. 그리고 표본의 크기와 그룹의 성질에 따라 t 검정이 달라집니다.
- 독립표본 t 검정 : 독립 표본 t-검정은 두 개의 집단이 동일한 분산을 가진 경우(등분산, equal variance)와 두 개의 집단이 다른 분산을 가지고 있는 경우(이분산, unequal variance)가 있다
- 대응표본 t 검정 : 두 집단 간의 차이를 비교하는 독립 표본 t-test와는 달리, paired t-test는 같은 집단의 전후 차이를 비교한다. 특정 수업을 들은 전후의 성적 차이나, 약물 복용 후 효과 차이와 같은 것이 있을 수 있다.
- 카이제곱검정 : 카이제곱 통계량은 데이터 분포와 가정된 분포 사이의 차이를 나타내는 측정값으로 이 통계량이 카이제곱 분포를 따른다면 카이제곱분포를 사용해서 검정을 수행합니다. 카이제곱분포에서 일어나기 불가능한 일이면 귀무가설 기각, 대립가설 채택이 이루어집니다.
- 분산 분석(ANOVA, Analysis of variance) : 3개 이상의 다수 집단을 비교할 때 사용하는 검정 방법으로 F분포를 사용합니다. 분산 분석은 집단 내 분산이 서로 비슷해야 비교가 가능한데 이것이 등분산성 가정이라고 합니다.

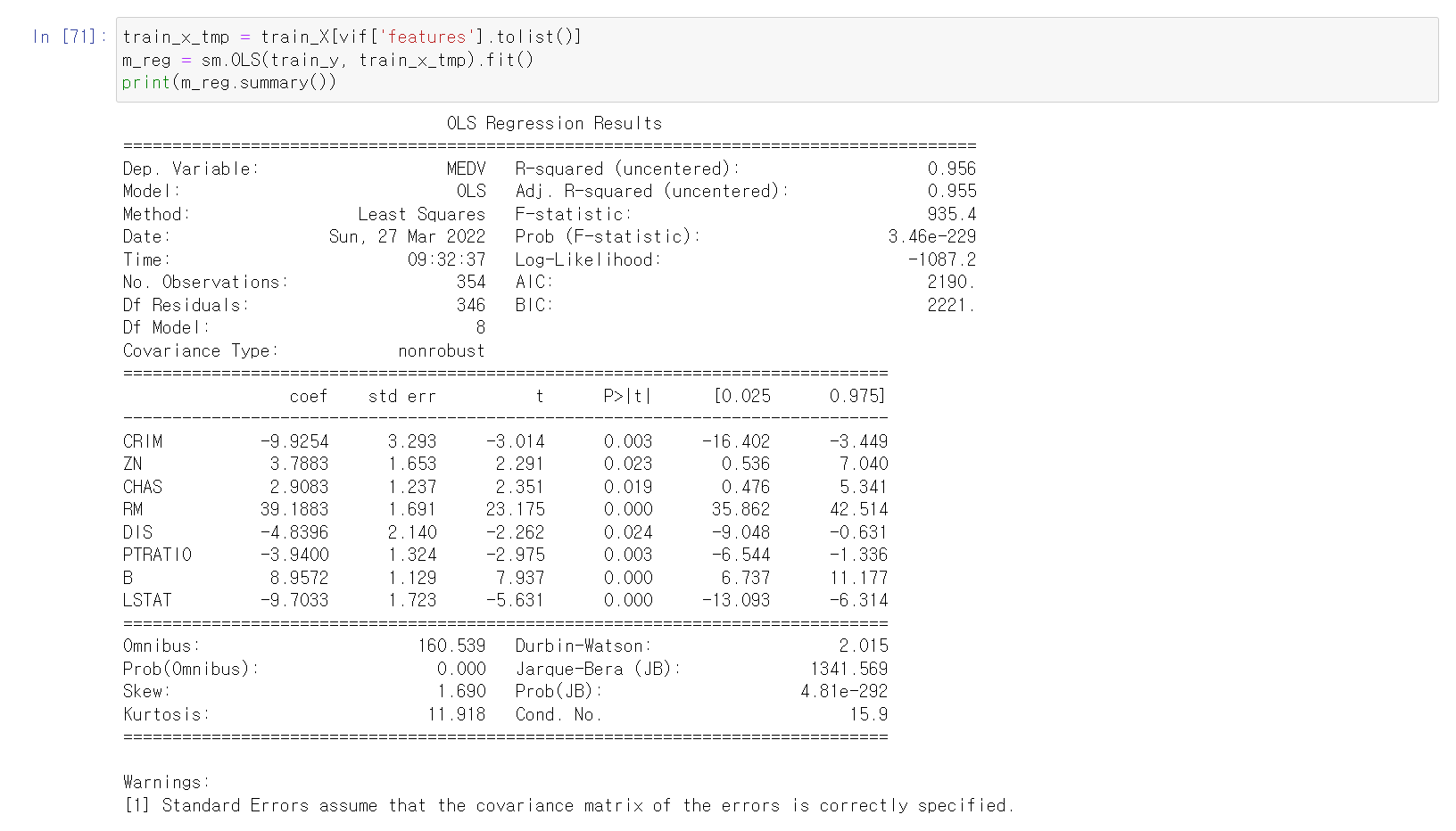
선형회귀분석
- 단순 선형회귀분석 : 보통 회귀라는 말은 원래의 상태로 돌아간다는 의미를 지니고 있으며 단순 선형회귀분석은 독립변수와 종속변수가 각각 하나씩 있는 분석입니다.
- 독립변수 : 독립변수는 영향을 미칠 것으로 생각되는 변수를 의미합니다.
- 종속변수 : 종속변수는 영향을 받을 것으로 생각되는 변수를 의미합니다.
- 회귀계수 : 'y = b0 + b1*x1'의 형태일 때 기울기 b1과 절편인 b0가 회귀 계수에 속합니다.
- 다중 선형회귀분석 : 이름과 같이 다중, 즉 여러 원인이 존재하는 경우에 대해 여러 독립변수를 준비하고 종속변수 y를 설명하는 회귀 방정식을 만드는 분석이다.
- 결정계수(R-Squared) - 독립변수가 종속변수를 얼마만큼 설명해 주는지를 가리키는 지표로서 퍼센트로 나타낼 수 있는데 그 값이 높을수록 상관관계가 높다고 말할 수 있다. 구하는 식은 R^2 = 1 - 'SSE/SST'인데 여기서 SSE(Explained Sum of Squares)는 추정값에서 관측값의 평균을 뺀 총합을 의미하고 SST(Total Sum of Squares)는 관측값에서 관측값의 평균을 뺀 결과의 총합을 의미합니다.

선형회귀의 기본적인 가정 5가지
- 선형성(Linearity) : 분석 시에 'y = b0 + b1*x1 + b2*x2 + b3*x3 + ··· + bn*xn'의 식을 만족하는 것을 의미합니다.
- 잔차 정규성(Normality) : 말 그대로 잔차는 정규분포를 이루어야 한다는 의미입니다.
- 독립성(Independence) : 다중 선형회귀에만 해당하는 가정으로 독립변수들은 서로 독립적이어야 한다는 의미입니다.
- 다중 공선성(Multicollinearity) : 다중 회귀분석을 수행할 경우 독립변수 간에 강한 상관관계가 없어야 된다는 의미입니다. 실제로 데이터 분석 시 상관관계가 높은 변수는 제거하고 분석하는 경우가 있습니다.
- 등분산성(Homoskedasticity) : 분산이 특정 패턴 없이 일정해야 한다는 의미입니다.
(오차(Error)는 모집단에서 회귀식을 얻어서 회귀실을 통해 얻은 예측값과 관측값의 차이이고 잔차(Residual)는 표본에서 회귀식을 얻어서 회귀식을 통해 얻은 예측값과 관측값의 차이를 의미합니다.)
- RMSE : 이상치가 많을 때 값을 보정하기 위해 사용하는 실제값과 예측값의 비교할 때 사용되는 측도입니다. 식은 ((예측값-실제값)^2/예측개수)^1/2입니다.
기초 수학 및 통계
함수
- Relation : 우선 relation은 관계라는 의미를 가지고 있는데 수업 중에 강사님은 A relation R의 정의를 A, B라는 집합이 존재할 때 AxB의 부분집합이라고 했습니다. 이 말은 관계라는 의미대로 relation은 하나로 이어진다는 느낌을 받았습니다.
- Domain, Codomain, Range(or image) : Domain은 정의역이고 Codomain은 공역이고 Range는 치역을 의미한다. 오늘 수업에서 중요하게 다뤘던 부분은 치역은 f(x)로 그 자체로는 함수가 될 수 있다고 하셨다.
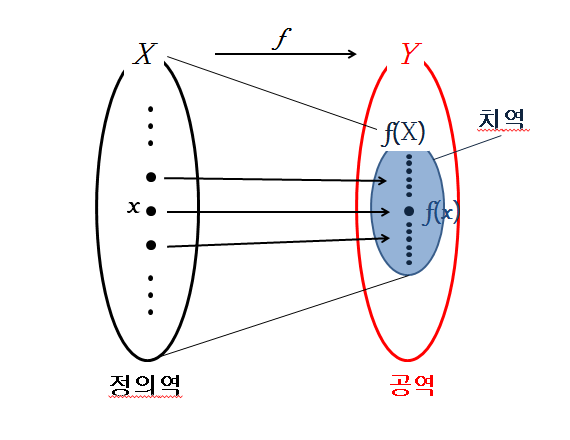
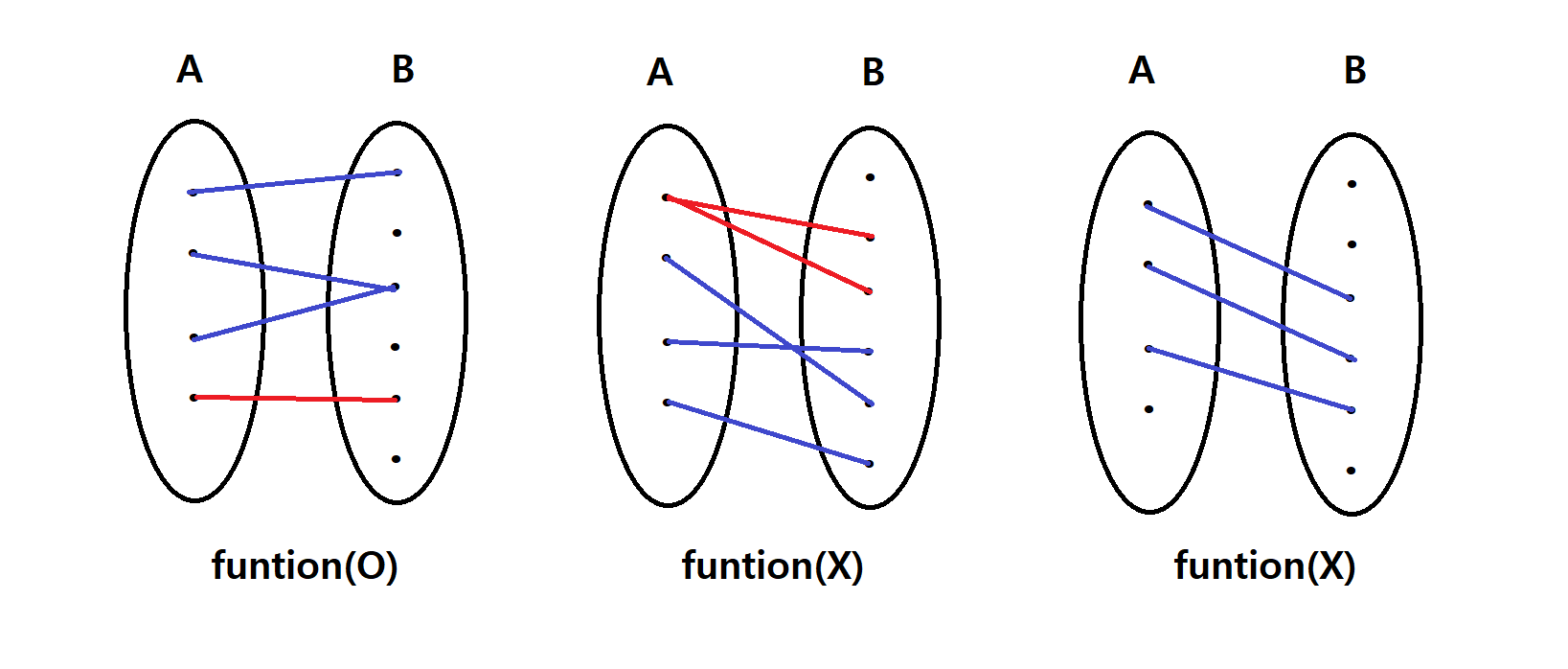
- 함수의 조건 : 치역에 관한 이야기를 하면서 자연스럽게 함수가 되는 조건에 대한 이야기가 나왔는데 함수라는 것은 영어로 'if for each x∈A, there exists a unique element y∈B such that (x, y)∈f '라고 나와 있는데 수식적으로 표현해 보자면 f: A→B and y=f(x) if (x, y)∈f라고 한다. 처음에 글자 그대로 해석하자면 유니크한 원소를 가지고 있는 것이 함수라는 의미였다. 처음 글자만 봤을 때는 이해가 잘 되지 않았지만 그림을 보면 이해가 될 것입니다.
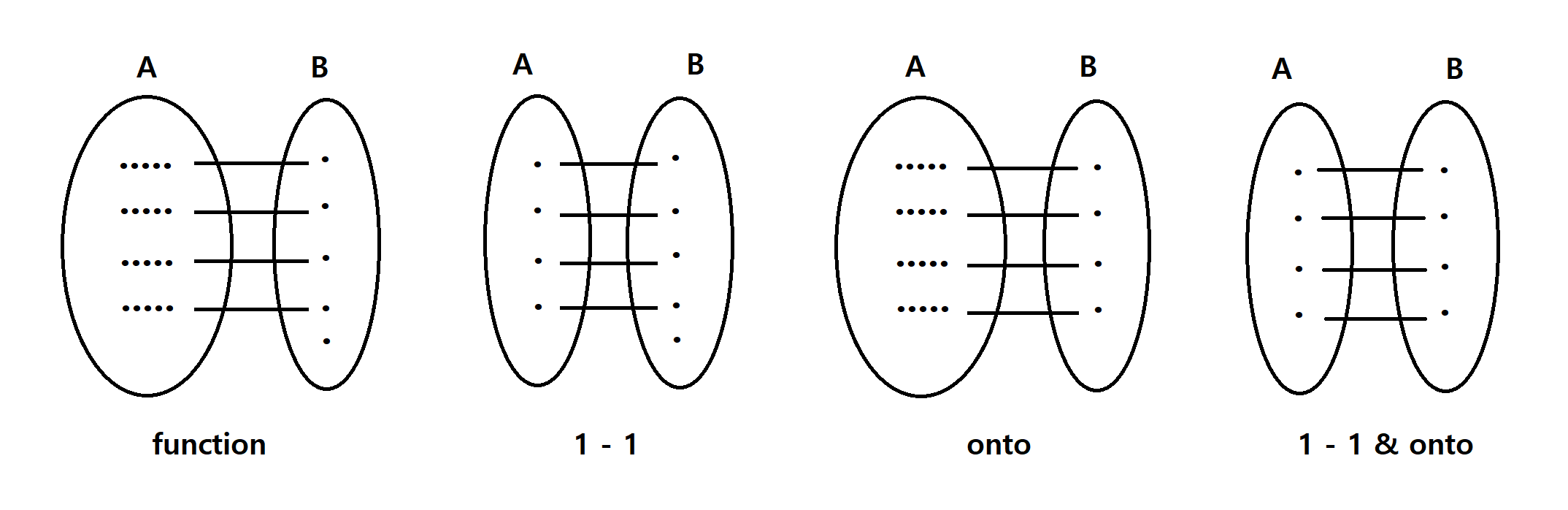
- One-to-one(1-1, injective), onto(surjective), 1-1& onto의 정의 : 그림으로 설명
확률 기초
- sample space : the total set for all observation data
- event : a subset of the total space
그 밖의 용어 정리
A := B의 의미 : B is defined by A
∃! : uniquely exist
P ∈ [a, b] : {x ∈ R(실수)| a≤ x ≤ b}
uniform distribution : 균등분포라는 의미로서 분포가 특정 범위 내에서 균등하게 나타나 있을 경우를 가리킵니다. 균등분포는 특이하게 이산형확률분포, 연속형 확률분포 두 형태 모두가 존재하는데 표현식의 차이가 있을 뿐, 특정 범위 내에서 분포가 균등하게 나타난다는 개념은 동일합니다.
discrete random variable : 이산 확률 변수라고 하며 확률 변수 X가 취할 수 있는 모든 값을 x1, x2, x3,...처럼 셀 수 있을 때 X를 이산확률변수라고 한다. 유한개의 값(Finite), 혹은 자연수의 부분집합과 일대일 대응이 가능한(Countable, 혹은 시간이 얼마나 걸리더라도 분명히 셀 수 있는) 값으로 구성되어 있는 확률변수이다.
continuous random variable : 연속 확률 변수라고 하는데 적절한 구간 내의 모든 값을 취하는 확률 변수이다. 연속적인 범위의 값을 지니는 확률변수를 의미한다.
[마무리]
오늘은 3일 차 수업을 마무리했는데 아직까지 데이터 사이언스나 AI 분야를 위한 기초 통계학에 관한 수업이 주를 이루고 있습니다. 특히 기초 수학 강의에서는 비록 기초적인 부분이지만 중고등학교 시절 때보다도 더 심도 있게 학습을 하고 있다는 느낌을 받았습니다. 길게 본다면 앞으로 데이터 분석이나 프로그래밍 과정에서 여러 가지 어려운 상황에서 좀 더 논리적으로 해결할 수 있는 사고력에 도움이 될 것이라고 긍정적인 생각이 들었습니다.
'AI > 기초 이론' 카테고리의 다른 글
| [AI 부트캠프] DAY 6 - 기초 통계학 및 수학 이론 강의 5 (0) | 2023.07.24 |
|---|---|
| [AI 부트캠프] DAY 5 - 기초 통계학 및 수학 이론 강의 4 (0) | 2023.07.22 |
| [AI 부트캠프] DAY 4 - 기초 통계학 및 수학 이론 강의 3 (2) | 2023.07.21 |
| [AI 부트캠프] DAY 2 - 기초 통계학 및 수학 이론 강의 1 (1) | 2023.07.19 |




댓글