[오늘의 일지]
머신러닝 녹화 강의 - 머신러닝을 위한 개념 수업 (Classification)
[상세 내용]
머신러닝을 위한 개념
Classification
- Classification(분류)은 머신 러닝 및 통계 분석의 하위 분야로, 데이터 포인트를 여러 클래스 또는 범주 중 하나로 분류하는 작업을 의미합니다. Classification은 주어진 입력 데이터를 사전 정의된 범주 또는 레이블로 할당하는 과정입니다. 이렇게 할당된 클래스 또는 레이블은 데이터의 특성과 패턴을 기반으로 결정됩니다.
Classification를 위한 Loss Function
- Classification는 말 그대로 분류라는 의미이기 때문에 분류가 되었는지를 참으로 판단을 하는 로스 함수를 가지게 됩니다. 그 예시로는 불순도(Impurity)를 측정하는 방법이 있습니다.
Measuring Impurity for Split
- Gini Index (Max 0.5, 0일 때 가장 잘 나누어진 것)
- Entropy (0일 때 가장 잘 나누어진 것)
- Misclassification Error (잘 사용하지 않음)
Gini Index
- Gini Index(지니 지수)는 머신 러닝 및 통계에서 사용되는 지표 중 하나로, 데이터 집합의 불순도(impurity)를 측정하는 데 사용됩니다. 주로 분류(classification) 문제에서 결정 트리(Decision Tree) 알고리즘과 관련하여 사용됩니다. Gini Index는 데이터 집합의 혼합 정도를 나타내며, 값이 작을수록 데이터가 더 순수하게 분류되었음을 의미합니다.

Entropy
- 엔트로피는 확률 분포의 예측 가능성과 무질서도를 측정하는 데 도움을 줍니다. 정보 이론에서는 엔트로피를 최소화하거나 정보 이득을 최대화하기 위해 사용되는 중요한 개념 중 하나입니다. 아래는 이산 확률 분포의 엔트로피 공식입니다.

Decision Tree
- Decision Tree는 트리 구조로 표현되며, 각 노드(node)에서는 특정 특성(feature)에 대한 테스트(조건)가 수행됩니다. 테스트 결과에 따라 데이터는 트리의 가지(branch)를 따라 이동하며, 리프 노드(leaf node)에 도달하면 최종적인 예측 또는 분류 결과가 결정됩니다.
- Rule Extraction : 가장 중요하고 강력한 해석력을 가짐
- Simple 하지만 직관력이 있음 : Simple is the Best
- Model이 복잡해질수록 해석력은 현저히 떨어지게 됨

Decision Tree Split 하는 원리
- Root Node 설정 : 결정 트리의 시작점은 루트 노드(root node)입니다. 루트 노드는 모든 훈련 데이터 포인트를 포함하고 있으며, 모든 데이터 포인트에 대한 특성(feature) 값을 기반으로 분할 기준을 결정해야 합니다.
- 분할 기준(분할 조건) 선택 : 루트 노드에서는 어떤 특성과 어떤 값을 기준으로 데이터를 분할할지 선택해야 합니다. 이를 위해 모든 가능한 분할 기준을 고려하고, 각 분할 기준에 대한 불순도(impurity) 또는 정보 이득(information gain)을 계산합니다. 일반적으로 불순도가 낮아지거나 정보 이득이 최대화되는 분할 기준을 선택합니다.
- 불순도 계산 : 불순도는 데이터 분할의 품질을 측정하는 지표로, 주로 분류 문제에서 사용됩니다. 일반적인 불순도 지표로는 지니 지수(Gini Index), 엔트로피(Entropy) 등이 있습니다. 분할된 하위 노드의 불순도를 계산하여 이 지표를 최소화하려고 노력합니다.
- 분할 수행 : 선택한 분할 기준에 따라 데이터를 두 개 이상의 하위 그룹으로 분할합니다. 이때, 각 하위 그룹은 자식 노드(child node)로 나타내어집니다. 각 자식 노드는 분할한 데이터의 서브셋을 가지게 됩니다.
- 재귀적 분할 : 위의 단계를 자식 노드에 대해 재귀적으로 반복합니다. 각 자식 노드에 대해 다시 분할 기준을 선택하고, 데이터를 하위 그룹으로 분할합니다. 이러한 과정을 결정 트리가 완전히 성장하고 더 이상 분할이 불가능할 때까지 반복합니다.
- 종료 조건 : 분할 기준을 선택하고 데이터를 분할할 때 종료 조건을 만족하면 분할을 중단합니다. 종료 조건은 트리의 최대 깊이, 노드에 포함된 최소 데이터 수, 불순도의 임계값 등으로 설정됩니다.
- 트리 구성 : 위의 과정을 거치면 결정 트리가 생성됩니다. 이 결정 트리는 루트 노드에서부터 잎 노드(리프 노드)까지 이어지는 의사 결정 규칙을 포함하고 있습니다. 각 리프 노드는 예측 클래스 또는 값이 됩니다.
Classification Model 평가 및 지표 해석
Confusion Matrix
- TP(True Positive), 참 양성: 예측한 값이 Positive이고 실제 값도 Positive인 경우
- FN(False Negative), 거짓음성: 예측한 값이 Negative이고 실제 값은 Positive인 경우
- FP(False Positive), 거짓양성: 예측한 값이 Positive이고 실제 Negative값은 인 경우
- TN(True Negative), 참음성: 예측한 값이 Negative이고 실제 값도 Negative인 경우
- 정분류율(Accuracy) : 정확도는 직관적으로 모델 예측 성능을 나타내는 지표
- 정밀도(Precision): 예측 Positive 중 실제도 Positive를 찾아낸 비율 (미처 잡아내지 못한 개수가 많더라도 더 정확한 예측이 필요한 경우)
- 재현율(Recall): 실제 Positive 중 올바르게 Positive를 예측해 낸 비율 (잘못 걸러내는 비율이 높더라도 참 값을 놓치는 일이 없도록, 의학, 불량)
- 특이도(Specificity): 실제 Negative 중 올바르게 Negative를 찾아낸 비율

Ensemble
- Ensemble(앙상블)은 머신 러닝에서 사용되는 강력한 기술 중 하나로, 여러 개의 기본 모델(약한 학습자, weak learner)을 결합하여 더 강력하고 정확한 모델(강한 학습자, strong learner)을 생성하는 기법을 말합니다. Ensemble은 모델의 예측을 결합함으로써 단일 모델보다 더 좋은 성능을 달성하고, 예측의 안정성을 향상하는 데 사용됩니다.
Ensemble의 종류
- Bagging : Reduce the Variance
- Stacking : Use another prediction model
- Boosting : Reduce the Bias
Bagging
- Bagging은 Bootstrap Aggregating의 줄임말로, 머신 러닝에서 사용되는 Ensemble(앙상블) 기법 중 하나입니다. Bagging은 다수의 기본 모델(예: 결정 트리)을 병렬로 학습하고 그들의 예측을 결합하여 더 강력하고 안정적인 예측 모델을 생성하는 기법입니다.
Bagging의 원리
- 부트스트랩 샘플링 (Bootstrap Sampling) : 먼저, 원본 훈련 데이터셋으로부터 부트스트랩 샘플을 생성합니다. 부트스트랩 샘플은 원본 데이터에서 중복을 허용하고 무작위로 데이터 포인트를 복원 추출하여 만듭니다. 이로써 각 부트스트랩 샘플은 원본 데이터와 크기는 동일하지만 일부 데이터 포인트가 중복되거나 누락될 수 있습니다.
- 기본 모델 학습 : 생성된 부트스트랩 샘플을 사용하여 다수의 기본 모델(예: 결정 트리)을 독립적으로 학습합니다. 각 모델은 서로 다른 학습 데이터를 기반으로 학습되며, 모델 간의 다양성이 확보됩니다.
- 예측 수집 : 학습된 기본 모델은 테스트 데이터 또는 검증 데이터에 대한 예측을 수행합니다. 각 모델은 개별적으로 데이터를 예측하게 됩니다.
- 결합 (Aggregation) : 모든 기본 모델의 예측을 수집하고, 분류 문제에서는 다수결 투표를 사용하여 최종 예측 클래스를 선택하거나 회귀 문제에서는 예측값의 평균을 계산하여 최종 예측을 생성합니다. 이로써 다수의 모델의 의견을 종합하여 더 강력하고 안정적인 예측을 얻을 수 있습니다.
- 성능 평가 : 앙상블 모델의 성능은 보통 테스트 데이터나 교차 검증을 통해 평가됩니다. 평가 지표(예: 정확도, 평균 제곱 오차 등)를 사용하여 모델의 성능을 측정하고 최적화할 수 있습니다.
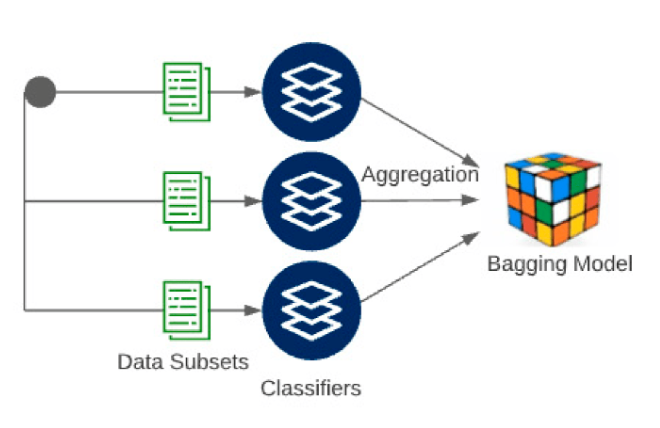
Random Forest
- 랜덤 포레스트(Random Forest)는 Ensemble 기법 중 하나로서 Bagging의 변형이며 , 여러 개의 결정 트리(Decision Tree)를 결합하여 더 강력하고 안정적인 예측 모델을 생성하는 머신 러닝 알고리즘입니다. 랜덤 포레스트는 무작위성(randomness)을 활용하여 다수의 결정 트리를 생성하고 이를 통합하여 과적합을 줄이고 일반화 성능을 향상합니다.
Random Forest – Out Of Bag 활용
- Bootstrap을 진행하면 확률 상 뽑히지 못한 데이터는 36.8%가 됨
- 뽑히지 못한 Data를 활용하여 Model의 성능을 측정함
- 대게 Model의 성능을 측정할 때, Train set과 Valid set을 나눔
- 하지만 Random Forest의 경우 Valid set을 나눌 필요가 없음 → 뽑히지 못한 36.8% OOB Data 활용
Random Forest - Feature Importance Score 계산법
- 랜덤 포레스트 학습: 먼저 랜덤 포레스트 모델을 학습합니다. 이 과정에서 결정 트리들이 생성되고 OOB 샘플이 생성됩니다.
- 각 결정 트리의 OOB 예측: 각 결정 트리에 대해 OOB 샘플을 사용하여 예측을 수행합니다. 이로써 각 결정 트리는 OOB 샘플에 대한 예측을 갖게 됩니다.
- 특성 중요도 계산: 각 특성의 중요도를 계산하기 위해 OOB 샘플을 사용한 결정 트리의 예측 오차를 측정합니다. 일반적으로 다음 두 가지 방법 중 하나를 사용합니다:
- 1. 순열 중요도(Permutation Importance): 각 특성을 무작위로 섞어서 OOB 예측을 다시 계산한 후, 예측 오차의 증가량을 측정합니다. 특성을 섞었을 때 모델의 성능이 떨어질수록 해당 특성은 중요한 것으로 간주됩니다.
- 2. OOB 예측 오차 감소(Decrease in OOB Prediction Error): 특정 특성을 사용한 결정 트리의 OOB 예측과 특성을 사용하지 않은 결정 트리의 OOB 예측 간의 오차를 측정합니다. 이 오차 감소량이 클수록 해당 특성은 중요하다고 판단됩니다.
- 평균화: 모든 결정 트리에서 계산된 특성 중요도를 평균화하여 최종 특성 중요도를 얻습니다.
Stacking
- 스태킹(Stacking), 또는 스태킹 앙상블(Stacking Ensemble)은 다양한 머신 러닝 모델을 조합하여 더 강력하고 정확한 모델을 만드는 앙상블 학습 기법입니다. 스태킹은 여러 다른 모델(기본 모델)을 학습하고, 그 결과를 기반으로 최종 예측 모델을 학습하는 방식으로 동작합니다. 이때, 최종 예측 모델을 "메타 모델"이라고 부르기도 합니다.
Stacking의 원리
- 첫 번째 레벨 모델 학습: 훈련 데이터를 사용하여 다양한 기본 모델을 학습합니다. 각 기본 모델은 다른 특성 엔지니어링이나 하이퍼파라미터 설정 등의 다양성을 가질 수 있습니다.
- 첫 번째 레벨 예측 생성: 학습된 기본 모델을 사용하여 검증 데이터 또는 홀드아웃 데이터에 대한 예측을 생성합니다. 이 예측은 메타 모델을 학습할 때 사용됩니다.
- 메타 모델 학습: 두 번째 레벨에서는 이전 단계에서 생성한 예측 결과를 사용하여 메타 모델(예: 선형 회귀, 결정 트리)을 학습합니다. 메타 모델은 최종 예측을 수행하는 주요 모델입니다.
- 최종 예측 생성: 테스트 데이터나 새로운 입력 데이터에 대한 최종 예측은 메타 모델을 사용하여 생성됩니다.

Boosting
- 부스팅(Boosting)은 앙상블 학습(Ensemble Learning) 기법 중 하나로, 약한 학습기(Weak Learner)들을 결합하여 강력한 학습기(Strong Learner)를 생성하는 방법입니다. 부스팅의 주요 목표는 이전 모델들이 놓친 샘플에 초점을 맞추어 모델을 개선하는 것입니다. 부스팅은 일련의 약한 학습기를 순차적으로 학습하고 예측을 수행하면서 가중치를 조절하여 학습 데이터에서 놓친 패턴을 더 잘 학습하도록 하는 기법입니다.
Boosting의 원리
- 약한 학습기: 부스팅은 일반적으로 약한 학습기를 사용합니다. 약한 학습기는 무작위 추측보다 조금 더 나은 성능을 내는 모델을 의미하며, 예를 들어 얕은 결정 트리나 선형 모델 등이 사용됩니다.
- 가중치 업데이트: 부스팅은 학습 데이터에서 오분류된 샘플의 가중치를 높이는 방식으로 모델을 업데이트합니다. 이렇게 하면 이전 모델에서 놓친 패턴에 더욱 집중할 수 있습니다.
- 순차적 학습: 부스팅은 이전 모델의 예측 결과를 바탕으로 새로운 모델을 학습합니다. 이러한 모델은 이전 모델의 오류를 보완하도록 조정됩니다.
- 자동 가중치 조절: 부스팅은 각 모델의 예측 결과와 실제 레이블을 비교하여 잘못 분류된 샘플에 대한 가중치를 높이거나 낮춥니다. 이렇게 하면 오분류된 샘플에 집중하여 모델을 향상합니다.
- 최종 예측: 부스팅은 순차적인 모델 학습을 거치고 나면 모든 모델의 예측 결과를 종합하여 최종 예측을 생성합니다.

Adaboost
- AdaBoost(Adaptive Boosting)는 부스팅(Boosting) 알고리즘 중 하나로, 약한 학습기(Weak Learner)들을 결합하여 강력한 학습기(Strong Learner)를 만드는 앙상블 학습 기법입니다. AdaBoost는 분류(Classification) 문제를 위한 알고리즘으로 시작되었지만, 회귀(Regression) 문제에도 확장되었습니다. 사실 위에서 설명하고 있는 부스팅의 원리가 Adaboost와 똑같다고 보시면 됩니다.
Gradient Boosting Machine
- Gradient Boosting Machine (GBM)은 Boosting 기반의 앙상블 학습 알고리즘 중 하나로, 약한 학습기(Weak Learner)들을 조합하여 강력한 학습 모델을 만드는 기법입니다. GBM은 예측 모델을 구성하는 데 그레디언트 부스팅(Gradient Boosting) 방식을 사용하며, 회귀 및 분류 문제에 모두 적용 가능합니다. Adaboost와의 차이점은 학습 방법, 가중치 업데이트 방식, 예측 오차 보정, 모델 복잡성 등 다양한 측면에서 나타납니다.
GBM의 원리
- 약한 학습기: GBM은 일련의 약한 학습기를 사용합니다. 이러한 약한 학습기는 보통 얕은 결정 트리(Decision Tree)입니다. 각 결정 트리는 데이터의 패턴을 학습하고 예측을 수행합니다.
- 그레디언트 부스팅: GBM은 그레디언트 부스팅 방식을 사용하여 학습됩니다. 이는 이전 모델의 오차(잔차)에 대한 그레디언트(기울기) 정보를 활용하여 모델을 학습하고 예측을 개선하는 방식입니다.
- 잔차 보정: GBM은 이전 모델에서 오분류된 샘플에 대한 가중치를 조정하여 모델을 학습합니다. 이를 통해 이전 모델이 놓친 패턴에 더욱 집중하고 예측 성능을 향상합니다.
- 순차적 학습: GBM은 이전 모델에서 학습된 결과를 바탕으로 새로운 모델을 순차적으로 학습합니다. 각 모델은 이전 모델에서의 오차를 보정하도록 학습됩니다.
- 최종 예측: GBM은 모든 약한 학습기의 예측 결과를 결합하여 최종 예측을 생성합니다. 각 모델의 예측 결과에 가중치를 부여하여 최종 예측을 만듭니다.
XGBoost
- XGBoost는 eXtreme Gradient Boosting의 줄임말로, 그레디언트 부스팅(Gradient Boosting) 알고리즘을 기반으로 한 강력한 앙상블 학습 기법입니다. XGBoost는 특히 분류(Classification) 및 회귀(Regression) 문제에서 높은 예측 성능을 제공하며, 데이터 과학 및 머신 러닝 대회에서 널리 사용되는 인기 있는 머신 러닝 라이브러리 중 하나입니다.
XGBoost의 원리
- 그레디언트 부스팅: XGBoost는 그레디언트 부스팅 방식을 사용하여 학습됩니다. 이전 모델에서의 예측 오차(잔차)에 대한 그레디언트 정보를 활용하여 모델을 학습하고 예측을 개선합니다.
- 정규화 및 과적합 제어: XGBoost는 트리의 깊이를 제한하거나 리프 노드의 최소 크기를 설정함으로써 모델의 복잡성을 제어하고 과적합을 방지할 수 있습니다.
- 자동 가중치 조절: XGBoost는 오분류된 샘플에 대한 가중치를 조절하면서 모델을 학습합니다. 이를 통해 이전 모델이 놓친 패턴에 더욱 집중할 수 있습니다.
- 다양한 손실 함수: XGBoost는 다양한 손실 함수(loss function)를 지원하여 회귀 및 분류 문제에 대한 커스터마이징이 가능합니다. 예를 들어, 이항 분류의 경우 로지스틱 손실을 사용할 수 있습니다.
- 병렬 처리 및 고속화: XGBoost는 병렬 처리를 효율적으로 수행하고, 하드웨어 가속 기술을 활용하여 학습 및 예측 속도를 향상합니다.
- 결측값 처리: XGBoost는 결측값(missing values)을 자동으로 처리할 수 있는 기능을 제공합니다.
- 특성 중요도 추정: XGBoost는 모델의 특성 중요도를 추정하여 어떤 특성이 예측에 가장 중요한 역할을 하는지 파악할 수 있습니다.
LightGBM
- LightGBM은 "Light Gradient Boosting Machine"의 약자로, 그레디언트 부스팅(Gradient Boosting) 알고리즘을 기반으로 한 고속 그레디언트 부스팅 프레임워크입니다. LightGBM은 분류(Classification)와 회귀(Regression) 문제를 해결하는 데 사용되며, 특히 대용량 데이터셋에서 뛰어난 성능을 보이는 것으로 유명합니다. 또한 LightGBM은 다양한 프로그래밍 언어(예: Python, R, C++)에서 사용할 수 있습니다.
LightGBM의 원리
- 히스토그램 기반 부스팅: LightGBM은 히스토그램 기반의 그레디언트 부스팅을 사용합니다. 이 방식은 데이터를 히스토그램으로 변환하여 빠른 학습과 예측을 가능하게 합니다.
- 리프 중심 트리 분할: LightGBM은 리프 중심(Leaf-wise)의 트리 분할 방식을 채택하며, 이를 통해 더 깊은 트리를 구성하고 예측 성능을 향상합니다.
- 카테고리컬 특성 지원: LightGBM은 카테고리컬 특성(범주형 데이터)을 효과적으로 다룰 수 있는 기능을 제공합니다.
- 병렬 처리 및 고속화: LightGBM은 다중 스레드 및 GPU 가속화를 지원하여 대용량 데이터셋에서도 빠른 학습과 예측을 가능하게 합니다.
- 자동 가중치 조절: LightGBM은 이전 모델에서의 예측 오차에 따라 샘플 가중치를 자동으로 조절하여 모델을 학습합니다.
- 조기 중단 기능: 조기 중단(early stopping) 기능을 활용하여 과적합을 방지하고 최적의 모델을 선택할 수 있습니다.
- 특성 중요도 추정: LightGBM은 모델의 특성 중요도를 추정하여 어떤 특성이 예측에 가장 중요한 역할을 하는지 확인할 수 있습니다.
- 자체 데이터 로딩 및 저장 포맷: LightGBM은 데이터를 효율적으로 로딩하고 저장할 수 있는 바이너리 데이터 포맷을 지원합니다.
Evolution of Algorithm from Decision Trees
- 현재는 아래의 그림에서 LGBM - CatB - NGB까지 더 빠르고 효율적인 알고리즘이 등장했다고 합니다.




용어정리
Bootstrap
- 부트스트랩(Bootstrap)은 통계학과 머신 러닝에서 사용되는 리샘플링 기법 중 하나로, 주어진 데이터셋으로부터 중복을 허용하여 샘플을 추출하는 방법을 말합니다. 부트스트랩은 주로 표본 분포나 신뢰 구간을 추정하는 데 사용됩니다.
Bootstrap의 사용 목적
- 신뢰 구간 추정: 부트스트랩을 사용하여 모집단 분포에서 통계량(예: 평균, 분산)의 신뢰 구간을 추정합니다. 이를 통해 통계적으로 유의한 추정값 범위를 계산할 수 있습니다.
- 통계적 가설 검정: 부트스트랩을 사용하여 가설 검정을 수행합니다. 이를 통해 모집단에서 특정 가설에 대한 통계적 유의성을 확인할 수 있습니다.
- 머신 러닝에서의 활용: 부트스트랩은 머신 러닝 모델의 성능 평가에도 사용됩니다. 예를 들어, 리샘플링을 통해 여러 번의 모델 학습과 검증을 수행하여 모델의 성능을 평가하고 일반화 성능을 추정할 수 있습니다.
[마무리]
오늘도 머신러닝을 위한 중요한 개념 수업을 들었습니다. 오늘 수업을 들어보고 알게 되었는데 데이터의 종류가 어떤 것인지에 따라 활용해야 할 알고리즘 라이브러리들이 엄청나게 많다는 것을 알게 되었습니다. 그래서 지금은 일단 많은 개념에 익숙해지기 위해서 그냥 자주 접하는 방법밖에 없을 거 같습니다.
'AI > 머신러닝' 카테고리의 다른 글
| [AI 부트캠프] DAY 51 - 머신러닝 6 (0) | 2023.09.27 |
|---|---|
| [AI 부트캠프] DAY 50 - 머신러닝 5 (0) | 2023.09.26 |
| [AI 부트캠프] DAY 49 - 머신러닝 4 (0) | 2023.09.23 |
| [AI 부트캠프] DAY 48 - 머신러닝 3 (0) | 2023.09.22 |
| [AI 부트캠프] DAY 46 - 머신러닝 1 (0) | 2023.09.20 |




댓글